Deep Learning for Guitar Effect Emulation
Published 2020-05-10
Since the 1940s, electric guitarists, keyboardists, and other instrumentalists have been using effects pedals, devices that modify the sound of the original audio source. Typical effects include distortion, compression, chorus, reverb, and delay. Early effects pedals consisted of basic analog circuits, often along with vacuum tubes, which were later replaced with transistors. Although many pedals today apply effects digitally with modern signal processing techniques, many purists argue that the sound of analog pedals can not be replaced by their digital counterparts. We’ll follow a deep learning approach to see if we can use machine learning to replicate the sound of an iconic analog effect pedal, the Ibanez Tube Screamer. This post will be mostly a reproduction of the work done by Alec Wright et al. in Real-Time Guitar Amplifier Emulation with Deep Learning (Wright et al., 2020).
The code for this model (and training data) is available here: github.com/teddykoker/pedalnet.
Data
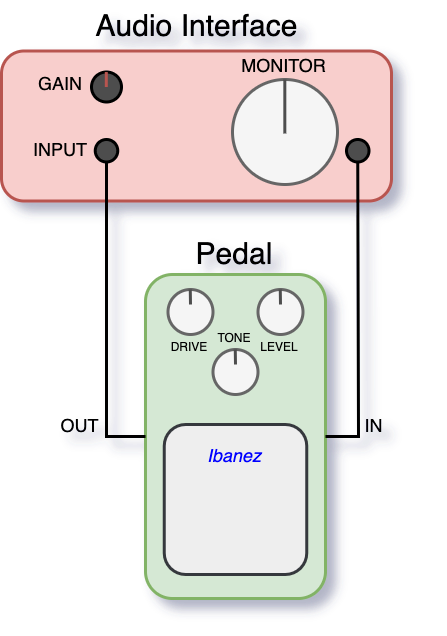
Popularized by blues guitarist Stevie Ray Vaughan, the Ibanez Tube Screamer is used by many well known guitarists including Gary Clark Jr., The Edge (U2), Noel Gallagher (Oasis), Billie Joe Armstrong (Green Day), John Mayer, Eric Johnson, Carlos Santana, and many more (Wikipedia, 2020). Using my own Ibanez TS9 Tube Screamer, we collect data by connecting the pedal to an audio interface and recording the output of a dataset of prerecorded guitar playing. The IDMT-SMT-Guitar dataset contains dry signal recordings of many different electric guitars with both monophonic and polyphonic phrases over different genres and playing techniques (Kehling et al., 2014). We’ll use a 5 minute subset of this data, and store both the original audio as well as the output of the pedal when the audio is passed through it. To maintain reproducibility, we set all of the knobs on both the pedal and audio interface to 12 o’clock:
Model
Our model architecture will be nearly identical to that of WaveNet: A Generative Model for Raw Audio (Oord et al., 2016). WaveNet models are able to generate audio that is both qualitatively and quantitatively better than more traditional LSTM and statistical-based models.
Dilated Convolutions
The “main ingredient” of the WaveNet architecture consists of a stack of dilated convolutions, or à trous, layers. By doubling the dilation – increasing the spacing between each parameter in the filter – for each layer , the receptive field of the model grows exponentially with depth of the model. This allows for computationally efficient models with large receptive fields, which is needed for audio effect emulation.
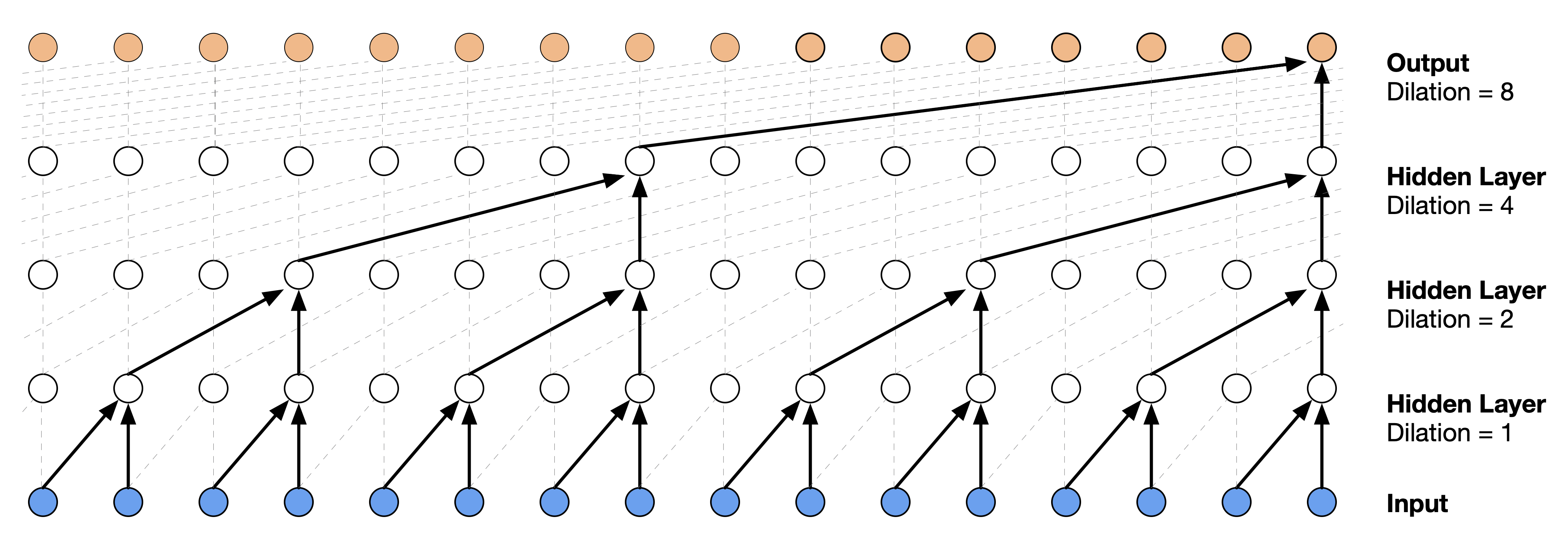 Figure 3 from WaveNet: Visualization of a
stack of dilated convolutional layers.
Figure 3 from WaveNet: Visualization of a
stack of dilated convolutional layers.
Gated Activation Units
Another notable feature of WaveNet architecture is the gated activation unit. The output of each layer is computed as:
\[z = \tanh \left(W_{f, k} \ast x\right) \odot \sigma \left(W_{g, k} \ast x \right)\]where $\ast$, $\odot$, and $\sigma(\cdot)$ denote convolution, element-wise multiplication, and the sigmoid function, respectively. $W_{f, k}$ and $W_{g, k}$ are the learned convolutionial filters at layer $k$. This was found to produce better results than the traditionally used rectified linear activation unit (ReLU).
Differences From WaveNet
The WaveNet model originally quantizes 16-bit audio time samples into 256 bins, and the model is trained to produce a probability distribution over these 256 possible values. In order to reduce the size of the model and increase its inference speed, we replace the 256 channel discrete output with a single continuous output. This is done by performing a $1 \times 1$ convolution on the concatenation of each layer’s output.
Training
To train our network, we minimize error-to-signal ratio. This is similar to Mean Squared Error (MSE), however the addition of the term in the denominator normalizes the loss with respect to the amplitude of the target signal:
\[L_\text{ESR} = \frac {\sum_{t} (H(y_t) - H(\hat{y}_t))^2} {\sum_{t} H(y_t)^2}\]where $\hat{y}$ is the predicted signal, and $y$ is the original output of the guitar pedal. $H(\cdot)$ is a pre-emphasis filter to emphasize frequencies within the audible spectrum:
\[H(z_t) = 1 - 0.95 z_{t-1}\]When selecting the number of layers and channels for the model, we find that a a stack of 24 layers, each with 16 channels, and a dilatation pattern of:
\[1, 2, 4,..., 256, 1, 2, 4,..., 256, 1, 2, 4, ..., 256\]was capable of replicating the sound well, while being small enough to run in real time on a CPU. The model is then trained for 1500 epochs using the Adam optimizer. This takes about 2 hours on a single Nvidia 2070 GPU.
Results
After training our network, we can listen to the models performance on the held-out test set. See if you can differentiate between Output A and Output B (you may need to wear headphones).
Input (Dry Signal)
Output A
Output B
Reveal Outputs
Output A is from the neural net; Output B is from the
real pedal.
We find that the model is able to reproduce a sound nearly indistinguishable from the real analog pedal. Best of all, the model is small and efficient enough to be used in real time. Using this technique, many analog effect pedals can likely be modeled with just a few minutes of sample audio.
As always, thank you for reading! For any questions regarding this post or others, feel free to reach out on twitter: @teddykoker.
- Wright, A., Damskägg, E.-P., Juvela, L., & Välimäki, V. (2020). Real-time guitar amplifier emulation with deep learning. Applied Sciences, 10(3), 766.
- Wikipedia. (2020). Ibanez Tube Screamer. https://en.wikipedia.org/wiki/Ibanez_Tube_Screamer
- Kehling, C., Abeßer, J., Dittmar, C., & Schuller, G. (2014). Automatic Tablature Transcription of Electric Guitar Recordings by Estimation of Score-and Instrument-Related Parameters. DAFx, 219–226.
- Oord, A. van den, Dieleman, S., Zen, H., Simonyan, K., Vinyals, O., Graves, A., Kalchbrenner, N., Senior, A., & Kavukcuoglu, K. (2016). Wavenet: A generative model for raw audio. ArXiv Preprint ArXiv:1609.03499.